La négation logique
Un paradoxe logique trompeur ( en haut page droite): I- Nous nous situons sur une surface, et nous nous intéressons à une division de cette surface totale (notée : 1) en deux zones, l'une absente ( -x) et l'autre tout ce qui n'est pas x (s'il était présent) soit ¬ x (lire : non x) ainsi nous pouvons écrire que 1 = ¬ x + (- x) qui se tranforme en 1 = ¬ x - x pour aboutir à ¬ x = 1 + x . Avant de progresser vers le second terme du paradoxe de la négation logique, nous devons oberserver que le raisonnement précédent s'opère sur une surface deux fois trouée, l'une en son centre ( x absent) et l'autre en son périmètre, périmètre comme bord d'une autre trou. Soit une tore. (voir les transformation topologique de la sphère vers le tore ). Ici nous notons que la surface ¬ x, dépend de l'objet manquant ayant laissé sa marque de trou - x ! 1 y est difinit par une absence ( - x) et par un contraire ( ce qui n'est pas x) ! et que cet objet manquant, x, dépend de la surface ¬ x !
2- Cette surface ne présente de trou qu'à sa périphérie, c'est donc une sphère une fois trouée. Soit une surface. La logique qui s'y déploie est plus familière. La surface totale toujours notée 1, elle y est égale à ¬ x + x . La pastille x, présente, n'est qu'un tracé sur la surface, sans rutpture, et nous pouvons écrire 1 - x = ¬ x
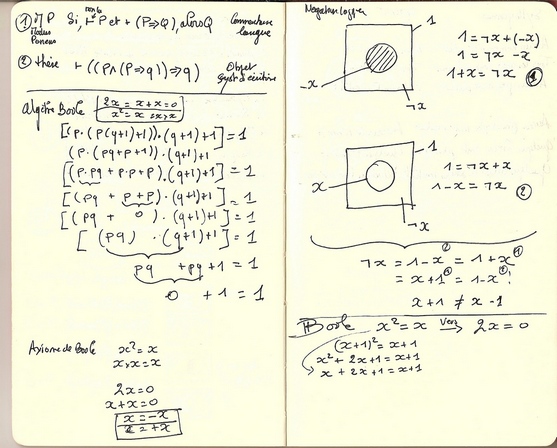
Nous arrivons à ce paradoxe apparent entre 1 et 2 : que ¬ x = 1 + x = 1 - x . Nous pouvons aussi écrire, les lois algébriques le permettant : x + 1 = 1 - x , cela est-il possible ? car nous devons pourtant aussi écrire en bonne logique que x + 1 ≠ x - 1 ! ? Et également x = - x ! ? Ce qui nous conduira à l'Axiome de Boole.
Interprétation : Nous voyons dans ce paradoxe, l'incidence d'un trou à peine masqué, celui qui nous entoure, et dans lequel nous somme, ce sera la droitre infinie de Lacan, thématisée D.I, par J-M.Vappereau (ici la périphérie de la page, ou du tableau) et d'autre part l'incidence d'un objet manquant (biface, - x) sur l'écriture de la surface apparente ( imaginaire/corps, théorie, monde) ici notée ¬ x. ( Nous y supposons l'incidence d'un phonème, de phonèmes insus ! et pourtant clef(s) !)